Universal Hopfield Networks: A General Framework for Single-Shot Associative Memory Models

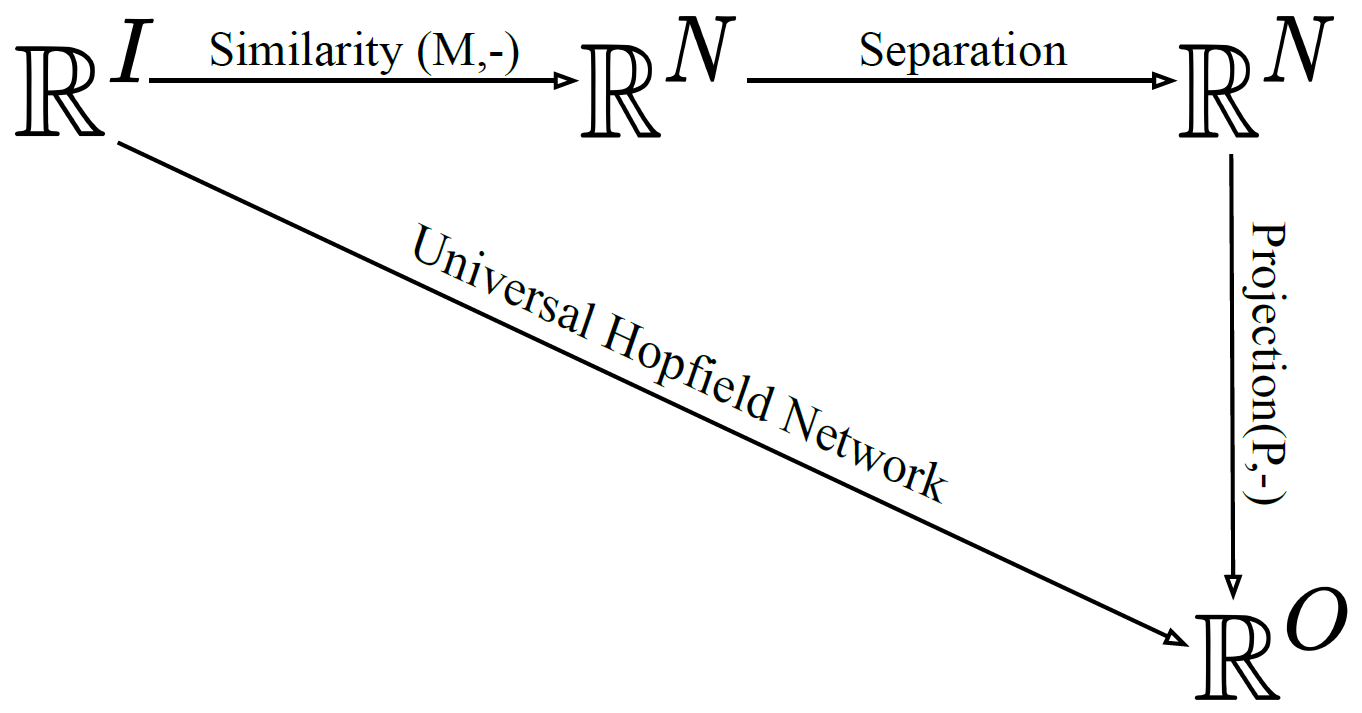
A large number of neural network models of associative memory have been proposed in the literature. These include the classical Hopfield networks (HNs), sparse distributed memories (SDMs), and more recently the modern continuous Hopfield networks (MCHNs), which possess close links with self-attention in machine learning. In this paper, we propose a general framework for understanding the operation of such memory networks as a sequence of three operations: similarity, separation, and projection. We derive all these memory models as instances of our general framework with differing similarity and separation functions. We extend the mathematical framework of Krotov et al (2020) to express general associative memory models using neural network dynamics with local computation, and derive a general energy function that is a Lyapunov function of the dynamics. Finally, using our framework, we empirically investigate the capacity of using different similarity functions for these associative memory models, beyond the dot product similarity measure, and demonstrate empirically that Euclidean or Manhattan distance similarity metrics perform substantially better in practice on many tasks, enabling a more robust retrieval and higher memory capacity than existing models.