Reverse Differentiation via Predictive Coding

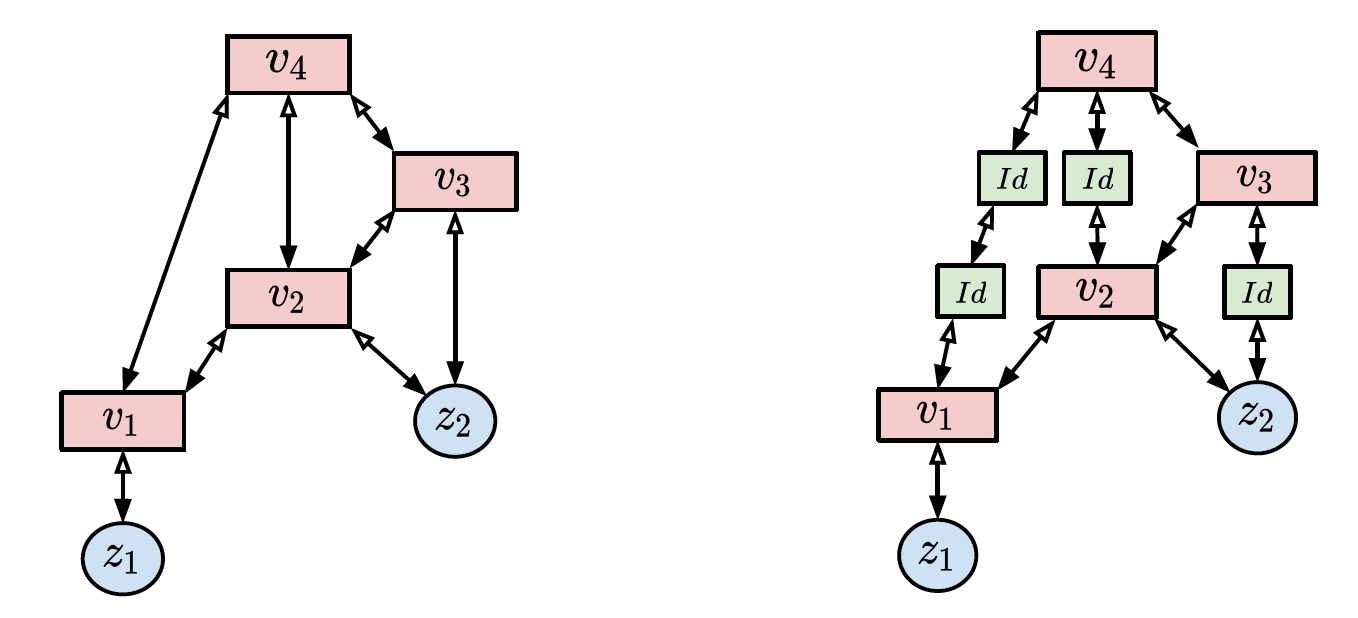
Deep learning has redefined AI thanks to the rise of artificial neural networks, which are inspired by neuronal networks in the brain. Through the years, these interactions between AI and neuroscience have brought immense benefits to both fields, allowing neural networks to be used in a plethora of applications. Neural networks use an efficient implementation of reverse differentiation, called backpropagation (BP). This algorithm, however, is often criticized for its biological implausibility (e.g., lack of local update rules for the parameters). Therefore, biologically plausible learning methods that rely on predictive coding (PC), a framework for describing information processing in the brain, are increasingly studied. Recent works prove that these methods can approximate BP up to a certain margin on multilayer perceptrons (MLPs), and asymptotically on any other complex model, and that zerodivergence inference learning (Z-IL), a variant of PC, is able to exactly implement BP on MLPs. However, the recent literature shows also that there is no biologically plausible method yet that can exactly replicate the weight update of BP on complex models. To fill this gap, in this paper, we generalize (PC and) Z-IL by directly defining it on computational graphs, and show that it can perform exact reverse differentiation. What results is the first PC (and so biologically plausible) algorithm that is equivalent to BP in the way of updating parameters on any neural network, providing a bridge between the interdisciplinary research of neuroscience and deep learning. Furthermore, the above results in particular also immediately provide a novel local and parallel implementation of BP.