Learning probability distributions of sensory inputs with Monte Carlo predictive coding.
When the brain processes sensory information, it makes educated guesses based on the noisy signals our senses provide. Traditionally, theories like predictive coding and neural sampling have explained parts of this process separately. This study merges these theories into one framework. This combined model closely matches the brain’s structure and activity, potentially improving our understanding of both neuroscience and machine learning.
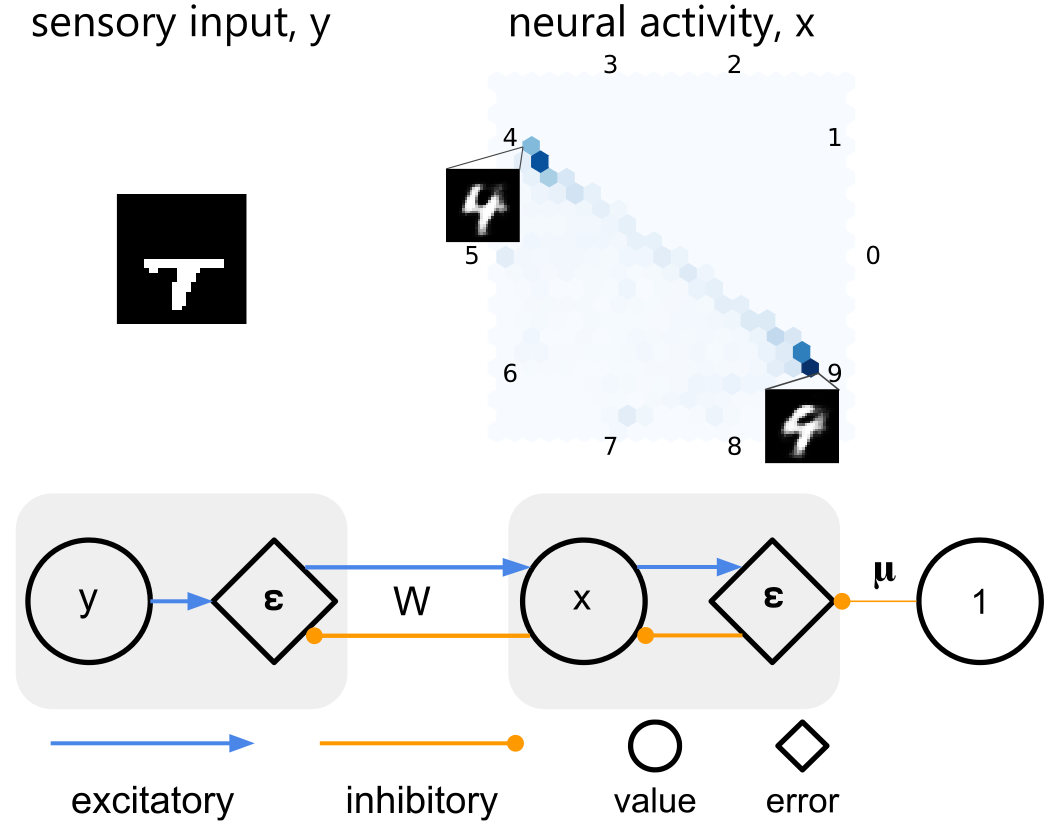
It has been suggested that the brain employs probabilistic generative models to optimally interpret sensory information. This hypothesis has been formalised in distinct frameworks, focusing on explaining separate phenomena. On one hand, classic predictive coding theory proposed how the probabilistic models can be learned by networks of neurons employing local synaptic plasticity. On the other hand, neural sampling theories have demonstrated how stochastic dynamics enable neural circuits to represent the posterior distributions of latent states of the environment. These frameworks were brought together by variational filtering that introduced neural sampling to predictive coding. Here, we consider a variant of variational filtering for static inputs, to which we refer as Monte Carlo predictive coding (MCPC). We demonstrate that the integration of predictive coding with neural sampling results in a neural network that learns precise generative models using local computation and plasticity. The neural dynamics of MCPC infer the posterior distributions of the latent states in the presence of sensory inputs, and can generate likely inputs in their absence. Furthermore, MCPC captures the experimental observations on the variability of neural activity during perceptual tasks. By combining predictive coding and neural sampling, MCPC can account for both sets of neural data that previously had been explained by these individual frameworks.
2024. PLoS Comput Biol, 20(10)e1012532.
2023. Adv Neural Inf Process Syst, 36:44341-44355.
2023. PLoS Comput Biol, 19(4)e1010719.
2017.J Math Psychol, 76(Pt B):198-211.