Properties of Neurons in External Globus Pallidus Can Support Optimal Action Selection.
Computer models suggest that, to select actions in the fastest possible way, a part of the brain called the external globus pallidus (GPe) must calculate a special mathematical function of the information it receives. Here, we modelled the results from experiments on real nerve cells to show that the connections and responses of two different types of GPe cell could best support action selection.
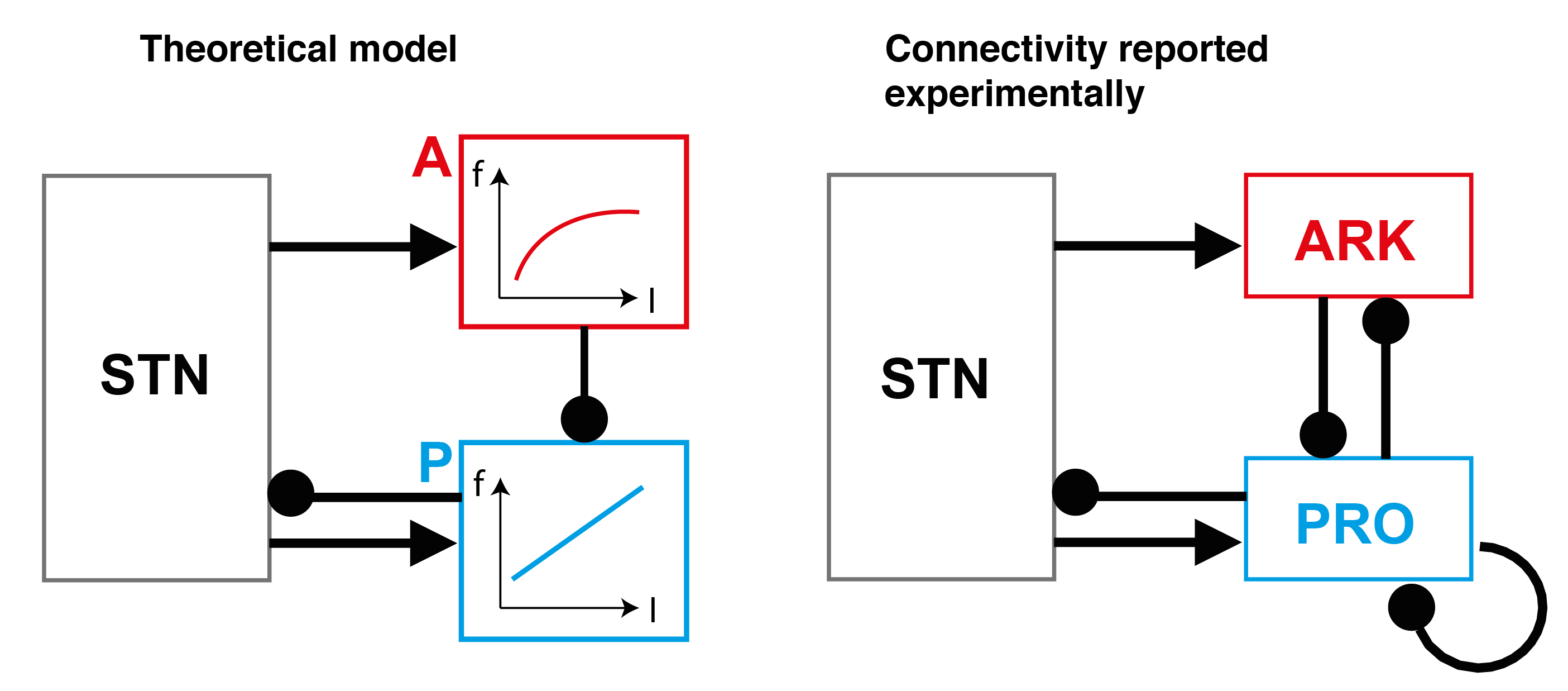
The external globus pallidus (GPe) is a key nucleus within basal ganglia circuits that are thought to be involved in action selection. A class of computational models assumes that, during action selection, the basal ganglia compute for all actions available in a given context the probabilities that they should be selected. These models suggest that a network of GPe and subthalamic nucleus (STN) neurons computes the normalization term in Bayes' equation. In order to perform such computation, the GPe needs to send feedback to the STN equal to a particular function of the activity of STN neurons. However, the complex form of this function makes it unlikely that individual GPe neurons, or even a single GPe cell type, could compute it. Here, we demonstrate how this function could be computed within a network containing two types of GABAergic GPe projection neuron, so-called 'prototypic' and 'arkypallidal' neurons, that have different response properties in vivo and distinct connections. We compare our model predictions with the experimentally-reported connectivity and input-output functions (f-I curves) of the two populations of GPe neurons. We show that, together, these dichotomous cell types fulfil the requirements necessary to compute the function needed for optimal action selection. We conclude that, by virtue of their distinct response properties and connectivities, a network of arkypallidal and prototypic GPe neurons comprises a neural substrate capable of supporting the computation of the posterior probabilities of actions.
2023. eNeuro, 10(7).